Introduction

Static typing is massively beneficial to the design and engineering of large systems: a good static type system can remove large classes of programming error before execution, clarify how pieces of a program fit together and enable fearless refactoring. Furthermore, type system can be more than just a safety nest: types provide “metadata” of sort to help development tools to know more about your code and enhance effectiveness, including smarter autocompletion engine, better suggestions from linter and even automated program synthesis in some case. The benefits of type systems go beyond pure programming: many approaches to domain-driven design also benefit from expressive type system as a domain modeling tool.

On the other side of the spectrum, dynamic typing are generally perceived as more flexible and faster to develop with. But the recent trend for many dynamically typed languages in common use are gradually shifting to “parially” static type to varying extent: either by using optional type specs/type hints like Elixir and Python, or by creating a full-blown backward-compatible statically typed language for an already existing dynamic language, in the case of Typescript and Javascript. As developers and software engineers at zen8labs, we’ve experienced first-hand this transition with Python and Javascript/Typescript and can testify for the ergonomics and productivity improvement.

On the other hand, a static type system too constrained may even reject logically correct programs. Most of the time, a too limiting (and limited) type system also reduces expressiveness which lead to code duplication. One proven approach to approximate the expressiveness of static languages to dynamic languages without sacrificing any of the benefits is to extend the type system with polymorphism.

Polymorphism

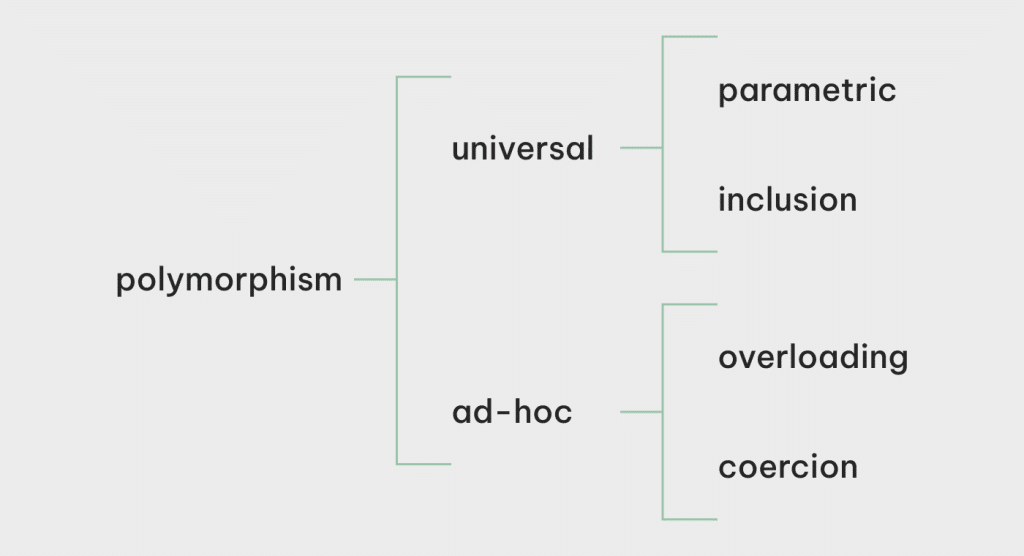
In programming context, polymorphism means a value or variable can have more than one type. According to Luca Cardelli’s seminal papers “On Understanding Types, Abstractions and Polymorphism”, there are 4 kinds of polymorphism:

• Parametric polymorphism: type of a variable/value can be parameterized over a range of types. Also more commonly known as generics.
• Inclusion polymorphism: types can be subtype of other types, and subtype can be used where supertype is expected. Also more commonly known as inheritance
• Overloading: one name/identifier can have multiple different definitions. Overloading exists in many incarnations in popular programming languages: overloaded methods (Java et al) and operators (C++), interface (Java et al), trait (Rust, Scala), protocol (Swift)… Most languages at least support some forms of numeric operator overloading, e.g. normally + can be applied to both floating point types and integral types. Sometimes + may even be overloaded with string concatenation too.
• Coercion: value of a concrete type can be converted into another concrete type and used in the context of that other type. Most languages support at least some form of coercion between numeric types.

The first two are also classified as universal polymosphism, while the last two are ad-hoc polymorphism Many popular languages have all 4 forms of polymorphism to varying extents, inducing interactions between them. As parametric polymorphism (generics) is the main focus of this blog post series, we’ll primarily explore the generics/overloading interactions in type bounds in part 1, and generics/inheritance interactions in variance in the upcoming part 2.

Generics

Let’s consider a motivating example using Golang, a major backend language in extensive use at zen8labs. Golang itself has very recently gone through the transition to incorporate generics into their language, so this example is gonna be something taken directly from production codebase. Suppose we want to write a function taking an array of string and returning the elements of that array satisfying a predicate:

func FilterString(f func(a string) bool, amap []string) []string {
	var res []string
	for _, v := range amap {
		if f(v) {
			res = append(res, v)
		}
	}
	return res
}

After a while, turns out we also need to filter array of integers too:

func FilterInt(f func(a int) bool, amap []int) []int {
	var res []int
	for _, v := range amap {
		if f(v) {
			res = append(res, v)
		}
	}
	return res
}

The two functions are structurally almost identical, the only difference is the type of the array’s element and correspondingly the input type of the predicate. In fact, we can have infinitely many such structurally identical functions for infitely many types. What we want is a way to universally abstract this same logic over all possible types, just like the way a function universally abstract the same logic over all possible values of its parameters. That’s where the “scientific ID” parametric polymorphism of generics came from. Consider the generic version of the Filter functions:

func Filter[T any](f func(a T) bool, amap []T) []T {
	var res []T
	for _, v := range amap {
		if f(v) {
			res = append(res, v)
		}
	}
	return res
}

A very observable change to the “monomorphic” versions is, we have [T any] instead of “String” and “Int” in the function name, and T now stands for the occurrences of string/int in type signatures in the function. T in this example is what we call a type parameter, because it is exactly like a function parameter, analoguous to how parameters are passed to functions at the more familiar value level. The [T any] construct introduces type parameter T to the rest of the following type signature, with any being a type bound or type constraint, which we’ll explore soon after this, for now it’s sufficient to read [T any] as “For all type T possible”.

While generics were remembered by most as being introduced by C++’s Template system in the early 90s, and later as its incarnation introduced in Java in 2004, the origin of generics went much further, with the term “parametric polymorphism” first appeared in 1967. The first programming language implemented parametric polymorphism was ML (MetaLanguage) in 1973, using the Hindley-Milner type system capable of full type inference for every definition and expression, meaning the compiler can infer the most general type even if your whole program never had any type annotation. This is not compatible with inheritance, so most modern programming languages with both generics and inheritance only restrict type inference to local variables. With full type inference, you can write statically typed programs without type annotations just like in dynamically typed languages.

Function/method’s type signature isn’t the only place where we can introduce type variables. Most languages with generics support also allow type parameters in type and interface definition:

public class ArrayList<E> extends AbstractList<E> implements List<E> {...}
public interface Collection<E> extends Iterable<E> {...}

Parametricity

When we have a family of structurally identical definition, we can generalize them into their generic version. It works the other way too: if you have a type signature of what your function/method should have, the number of possible valid implementations is typically restricted, since the definition must work universally for all possible types. Let’s look at the Filter example again: it takes an array of type T elements, and returns an array of type T elements. From the implementor’s point of view, there’s no way the function can create a value of any T possible out of thin air, so the returned elements can only be a combination of the input array’s elements. Or more interestingly, consider the following Map generic function:

func Map[A any, B any](f func(a A) B, aArray []A) []B {
    bArray := make([]B, len(aArray))
    for k, v := range aArray {
        bArray[k] = f(v)
    }
    return bArray
}

This function takes a function from A to B, and an array with A elements, and returns an array with B elements. Since it must be universally applicable to all A and B types possible, one can only implement it by applying the function from A to B to some elements of aArray to obtain some elements of type B to create bArray.

This property is called parametricity, and it can vastly improve reasoning and code comprehension: you can already tell a lot about the semantics of a piece of code just from its type signature, without even looking at its implementation. Some compilers even take advantage of it to do semantics preserving code transformations and optimizations.

Unfortunately, if a generic piece of code also uses facilities like reflection or type casting, then parametricity is lost: after all if you can tell what concrete type a type parameter is at runtime, you can call the corresponding constructor to create new values of that type out of thin air.

Parametricity: the phantom type pattern

One application of parametricity is the phantom type pattern. As the name suggest, a “phantom” type means a type parameter that doesn’t “materialize” anywhere in the generic type’s definition. Why would such a type parameter even be, well, not useless? Because we can use them to guarantee correctness at compile time. Consider the following Java snippet:

sealed interface Currency permits USD, VND {}
final class USD implements Currency {}
final class VND implements Currency {}
class Money<C extends Currency> {
  public int value;
  Money(int val) {
    this.value = val;
  }
} 

class Main {
  public static <C extends Currency> Money<C> add(Money<C> m1, Money<C> m2) {
    Money<C> total = new Money(m1.value);
    total.value = total.value + m2.value;
    return total;
  }

  public static void main(String[] args) {
    Money<USD> fund1 = new Money<USD>(1);
    Money<USD> fund2 = new Money<USD>(2);
    Money<VND> fund3 = new Money<VND>(1000);
    System.out.println(add(fund1, fund2).value);
    //System.out.println(add(fund3, fund2).value); // compilation error
  }
}

In the above snippet, we modeled Money as a wrapped integer value. Each Money value realistically should have its unit in some Currency, and we encoded that using a type parameter for the Money class: <C extends Currency> (this means Currency is an upper type bound for C, which we’ll explore in more detail in the next section). The type parameter C doesn’t appear anywhere in the definition of Money, but its use is in the signature of method add, to guarantee by parametricity that we can only add the value of a Money to another of the same Currency, to obtain a new Money value, still of that same Currency. So it’s fine to add 2 USD to 1 USD and obtain 3 USD, but it’s not possible to “accidentally” add 2 USD to 1000 VND, because they don’t share the same unit, and you’d probably have to convert that 2 USD to equivalent value in VND first.

While we can use an extra field in the Money class to tag each Money value with a particular Currency, this incurs non trivial runtime overhead, and most importantly the programmer must be mindful of checking that tag at runtime to, for example, prevent adding 1000 VND to 3 USD to obtain 1003 of … something invalid, because otherwise there really aren’t anything to prevent such operations. It’s a win to have compilers able to automatically check these kinds of thing for you instead. This is what functional programmers mean by “making invalid states unrepresentable” by leveraging the type system, which is an important tenet in functional programming, but still not yet widely known outside of that circle. The example above was intentionally written using Java as a demonstration that at the time of writing this blog post, this is no longer an “impractical practice” only possible in niche languages, and we can already apply this tenet to improve code correctness in even the most widely used OOP language of them all.

Bounds/Contraints

Sometimes the universal restriction of parametricity can be too strict, and we might need to be able to do more interesting things to the generic arguments the function received. We can achieve it with type bounds or type constraints.

The most commonly used kind of type bound is interface/protocol/trait implementation bound, meaning we can assert the type to be instantiated with the type variable must implements some overloading interface and thus the generic code can assume that type supports certain operations. Another common kind of bound is upper bound, where we assert the supertype the type extends. With these bounds, the implementation knows what operations/functions/methods can be used with the generic arguments. With different type systems, there may come other kinds of type bound too, like lifetime bounds in Rust, lower bound in Java or type equality bound in Haskell.

Existentials/Wildcards

Recall that type parameters are universally quantified: definition site of a generic value (e.g. the one who implemented the generic function like Filter above) can’t assume anything about the concrete type, while usage site (e.g. the caller of Filter) decides which type to instantiate the type parameters as.

We also have a dual notion to that in existential quantified types, where definition site of an existentially quantified value decides which type to instantiate, while usage site can’t assume anything. We can only claim that “there exists a type”, possibly satisfies certain type bound.

A familiar form of existentially quantified type is Java’s wildcard (<?>):

class Main {
  public static void printList(List<Object> ls) {
    System.out.println(ls);
  }

  public static <T> void genericPrintList(List<T> ls) {
    System.out.println(ls);
  }

  public static void main(String[] args) {
    List<?> ls = Arrays.asList(1,2,3,4); // definition site decides ls's type is List<int>
    //Main.printList(ls); // failed to compile, because you can't assume the wildcard <?> as type Object
    Main.genericPrintList(ls); // ok
  }
}

If the phrase “for all” and “there exists” ring familiar to you, then they probably are: these terms come directly from the good old “for all” and “there exists” in logic. We’ll come back to this later in part 2 of this blog post series.

What’s to expect in part 2

In the first part of this blog post series, we’ve learned what the types of polymorphism in programming are, and where generics stand among them. We then explored the motivation behind generics, how generics help with local reasoning of code and how type bounds and wildcards extend generics’ expressive power. In the next part of the series, we’ll delve deeper into generic programming and examine the many possible variance of a type variable, how generics are typically implemented, and as a bonus, some advanced and less discussed topics in generics programming – higher kinded type and higher ranked polymorphism.

Read Part 2 here!

Anh Ngo, Software Engineer