The story so far: in the Part 1 of this blog post series, we’ve learned what the types of polymorphism in programming are, and where generics stand among them. We then explored the motivation behind generics, how generics help with local reasoning of code and how type bounds and wildcards extend generics’ expressive power. In this second part of the series, we’ll delve deeper into generic programming and examine the many possible variance of a type variable, how generics are typically implemented, and as a bonus, some advanced and less discussed topics in generics programming – higher kinded type and higher ranked polymorphism.

Generics (cont.)

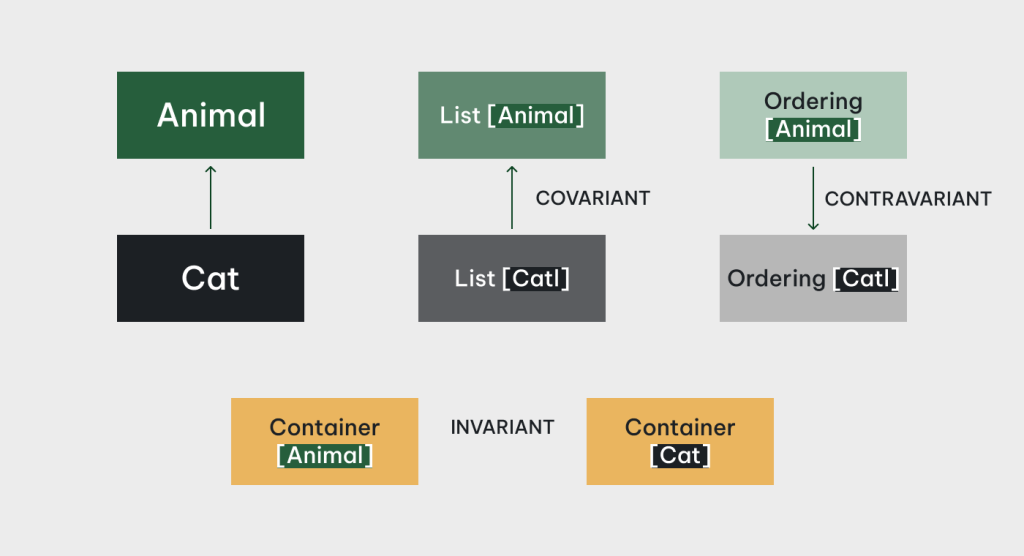
Variance: Co/Contra/Invariance

Let’s say we have an Animal type, with Dog and Cat as its subtypes, and we have a generic container type Container<A>. A problem arises: as we have Dog/Cat being subtypes of Animal, what is the right inheritance relationship between Container<Dog>/Container<Cat> and Container<Animal>? An intuitive and naive approach would be considering Container<Dog>/Container<Cat> also being subtypes of Container<Animal>, in academic jargons this kind of relationship is called covariance. As intuitive as it is, it may also unfortunately lead to inconsistency in the type system:

  class Main {
    class Container<A> {
      A item;
      Container(A item) {
        this.item = item; 
      }
    }
    class Animal {...}
    class Dog extends Animal {...}
    class Cat extends Animal {...}

    public static void swapAnimalInContainer(Container<Animal> c, Animal a) {
      c.item = a;
    }

    public static void main(String[] args) {
      Container<Dog> dogContainer = new Container<Dog>(new Dog()); // initialize a Container of some Dog 
      Cat aCat = new Cat();
      // dogContainer can be used as a Container<Animal>, and aCat can be used as an Animal, resulting in a Container<Dog> with a Cat in it! 
      // without saying that *should* result in runtime exception
      swapAnimalInContainer(dogContainer, cat);
    }
  }

What if we try the exact opposite of covariance (i.e. contravariance): making Container<Animal> a subtype of Container<Dog>/Container<Cat>?

  class Main {
    public static void main(String[] args) {
      Container<Animal> animalContainer = new Container<Animal>(new Cat()); // initialize a Container<Animnal>, with some Cat
      Container<Dog> dogContainer = animalContainer; // because Container<Animal> is a subtype of Container<Dog>
      Dog aDog = dogContainer.item // but this item is initialized as a cat!
    }
  }

This obviously still leads to type system inconsistency that in turn results in runtime exception. Curiously, in the former case we lose type safety under write, while in the latter case we lose type safety under read. Either way, does that mean there’s fundamentally no inheritance relationship between generic types instantiated with types in an inheritance hierarchy whatsover? Not necessarily so: sometimes the only relationship we can assert between type F<A> and F<B> given A and B is F<A> = F<B> iff A = B (we call these cases invariance), but there are natural covariances and contravariances in everyday programming. In fact, many modern programming languages with both generics and inheritance also have notation to mark whether a generic type’s type variables are covariant or contravariant w.r.t. that generic type, including but not limited to Scala, Kotlin, Swift and OCaml. In the coming examples we’ll use Scala’s syntax for similarity to Java, and its brevity in expressing co/contravariance: covariant mark being + and contravariant mark being -.

First let’s take another look the covariant case above. Observe that the root cause of type safety loss is the mutation of Container<A> values. If the type is immutable, there is no unsafe write, and we can safely use the type as being covariant in A. More concretely in Scala:

  class Container[+A](val item: A) {
  }

  sealed trait Animal {...}
  case class Dog extends Animal {}
  case class Cat extends Animal {}
  
  object Container {
    // compilation error: mutating immutable data
    //def swapAnimal(c: Container[Animal], a: Animal) {
    //  c.item = a 
    //}
  
    def main() {
      val dogContainer : Container[Dog] = new Container(Dog()) // initialize a Container of some Dog 
      val aCat = Cat()
      // swapAnimal(dogContainer, aCat) // compilation error: mutating immutable data
      // since it's impossible to add aCat into a Container[Dog], we can't get into the invalid state in the corresponding Java example
    }
  }

For the contravariant case, we can’t just contravariantly mark A as -A like in the covariant case, since Scala’s type checker would complain that we are using a contravariant type parameter in covariant position. What does this even mean? To put it simply, a type is in covariant position when we can sort of “produce” a value of that type from the given “outer” type, e.g. we can get the field val item: A given a value of type Container[A]. In contrast, a type is in contravariant position when we can sort of “consume” a value of that type using the given “outer” type. How does a type even “consume” another type? In general, by using its member functions, and in an OOP setting, also by using its methods:

  class Consumer[-A] {
    def consume(a: A) {
      // do something to a 
    }
  }

  object Consumer {
    def main() {
      val animalConsumer : Consumer[Animal] = new Consumer() // initialize a Consumer[Animal]
      val dogConsumer : Consumer[Dog] = animalConsumser // since Consumer[Animal] is a subtype of Consumer[Dog]
      dogConsumer.consume(Dog())
    }
  }

Using this same line of reasoning, we can understand why mutable generic types like Container<A> in the Java example must be invariant: the A member field is in covariant position, but you can consume its value by mutating it to another value, which should make it contravariant, so type parameter A must be invariant. For historical reason, Array and only Array in Java is covariant, which led to countless troubles in the past.

There’s one commonly arisen trouble with variance. Consider the Container class above, naturally we would like to have an insert method to extend a Container with a new element:

class Container[+A](val item: A) {
    def insert[A](elem : A) : Container[A] {...} // error: contravariant type A occurs in covariant position
  }

The problem with insert‘s type signature is, we declared A as covariant, but we use A in contravariant position (elem: A). This is a type error for the same reason that using covariance with mutation causes type error: you can create a Container of Dog with a Cat in it. So how do we write the “simple” code of inserting a Cat to a Container[Cat] in a type consistent way? By clever use of type bound:

  class Container[+A](val item: A) {
    def insert[S :> A](elem : S) : Container[S] {...}
  }

This method insert no longer consumes an A and return a Container[A], and uses an S that is an upper bound (supertype) of A instead. Obviously inserting a Cat to a Container[Cat] is allowed, but now if you try to insert a Dog to a Container[Cat], the type system would infer S to be Animal, since Animal is a supertype of Cat and a Dog is an Animal. The result is then a Container[Animal], so type safety is still guaranteed.

In some languages with the so-called use site variance annotation like Java, we can only specify variance at method definition (since generic classes and interfaces don’t have a way to annotate variance) using bounded wildcard, like the signature of the standard library method Collection.addAll: public static <T> boolean addAll(Collection<? super T> c, T... elements). It’s not as clean and succinct as the analogous method in Scala, but their goals coincided: you won’t find yourself inserting a Cat into a Collection<Dog>, but instead a Collection of some unknown supertype of Cat.

If everything in this section about variance seems complex or even convoluted, it’s probably because it genuinely and inherently is. The interplay between generics and inheritance is among the most complex features of mainstream programming languages. As intimidating as the variances are, understanding them would entail a deeper appreciation of relations between types (sub/supertype relations in OOP languages for example) and help us developers write code that are both more expressive and type safe.

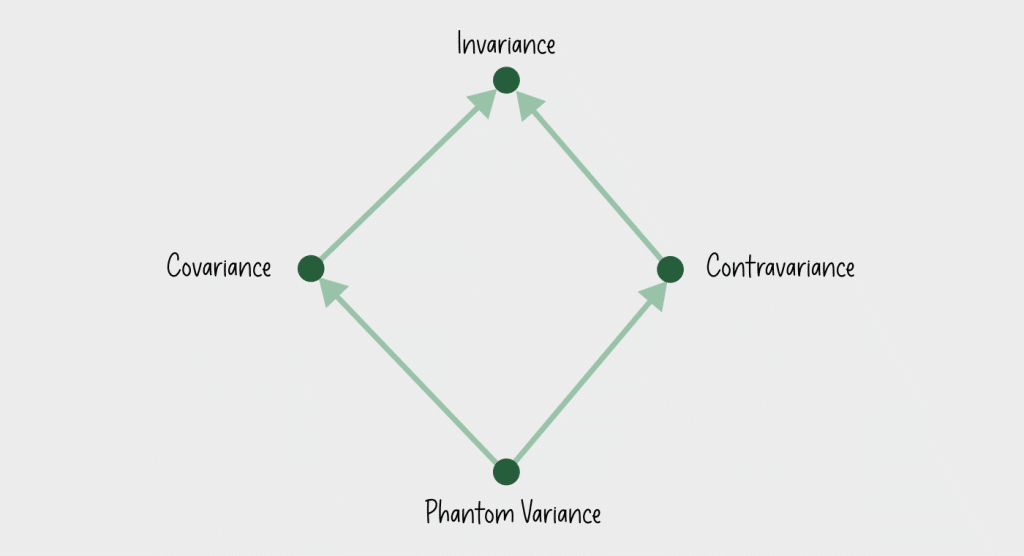
The astute readers might have realized that covariance, contravariance and invariance are insufficient to correctly model phantom type’s behavior: covariant type parameters must only appear in covariant position, contravariant must only appear in contravariant position, invariant must appear in both positions (or else it must either be co-or contra-variant instead). Because a phantom type parameter never appears anywhere in the generic type’s definition, it’s neither in covariant or contravariant position, thus it also isn’t invariant. We call this phantom variance, and currently the only language supporting phantom variance annotation in industrial use is Haskell, but it doesn’t have inheritance, in fact it isn’t object-oriented at all. Phantom variance currently has limited use and is only mentioned for completeness, thus won’t be discussed further in this blog post series.

Implementation and efficiency

Hopefully at this point we’ve all come to the agreement that generics is a great abstraction that can profoundly improves both code quality, safety and the language’s modelling power. But don’t all abstractions come at a cost? Not the case for so-called “zero cost abstractions” like generics! At least, not runtime cost, thanks to two commonly used implementation strategies: monomorphization and type erasure.

Monomorphization

“Monomorphic” is the opposite of “polymorphic”, and the act of “monomorphization” is to make polymorphic code into monomorphic code. What that means here is, during compilation the compiler takes generic code at each use site, specialize it to the concrete type being instantiated there to generate corresponding monomorphic code instead. For example, the generic Filter function earlier in the first part of this blog post series would reversely be transformed into function similar to the monomorphic FilterInt and FilterString to be used at call site with Int and String being instantiated, respectively.

Since generic code is transformed into its monomorphic counterpart anyway, there’s just no performance penalty at all. Instead, it takes more compilation time for code generation, and with all the code duplication, build artifacts generally take more space than the alternative: type erasure.

Type erasure

In languages where most (if not all) values are “boxed” into homogenous references e.g. Java, we can alternatively implement generics by erasing type information and everything is left as homogenous pointer of same size and layout pointing to heterogenous actual object with different layout elsewhere in memory. The erasure happens after type checking is done, so type safety isn’t compromised. Effectively, instead of going from “polymorphic type” to “monomorphic type”, this is a more drastic transformation from polymorphism to uni/untypeness.

This has obvious upside to monomorphization, since there’s no need to generate the almost identical code over and over again for different instantiated types, thus remarkably reduces build products size. There is of course a trade off here: since everything must be boxed and effectively is used as a pointer, it incurs all of the overhead associated with pointer indirection, plus the allocation for pointers themselves when it could be sufficient to directly use the unboxed, raw value.

Most modern languages that don’t have to concern themselves with squeezing out every last bit of efficiency implement generics by type erasure though, since it’s generally easier to use type erasure to implement other advanced type system features, such as higher ranked polymorphism. On the other hand, monomorphization can enable better code optimization at later phases of compilation, because there’s more specific type information at each use site, so the compiler has more information to decide which optimization to apply accordingly.

Beyond generics

Higher kinded type

Generics as commonly implemented is still not the complete form of parametric polymorphism. For example, going back to the analogy with value level function, we can see generic types as functions from type to type. Following this analogy even further, can we have something corresponding to higher order functions, i.e. functions that can take and/or return other functions? At the type level, that means a generic type that can be parameterized with other generic type, resulting in a new generic type. We call this higher kinded type. The only two languages currently in industrial use with higher kinded type are Haskell and Scala, this blog post will continue to use examples in Scala for the sake of consistency.

Higher kinded type has many advanced applications, most prominently for defining highly generic and reusable interfaces. Let’s take a look at an example of an interface (trait in Scala) for collection/container types that we can map over i.e. transform each element of the collection/container using a given function:

  trait Mappable[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
  }

  object Main {
    // implementation for Option
    implicit val functorForOption: Mappable[Option] = new Mappable[Option] {
      def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa match {
        case None    => None
        case Some(a) => Some(f(a))
      }
    }

    // implementation for List
    implicit val functorForList: Mappable[List] = new Mappable[List] {
      def map[A, B](la: List[A])(f: A => B): List[B] = la match {
        case Nil    => Nil
        case a :: rest => f(a) :: map(rest)(f)
      }
    } 

    // higher kinded typed map, works with every generic type that implements Mappable
    def fmap[T[_], A, B](t: T[A])(f: A => B)(implicit m : Mappable[T]): T[B] = {
      m.map(t)(f)
    }

    def main(args: Array[String]): Unit = {    
      val mappedList = fmap(List(1,2,3))(_ + 1) // List(2,3,4)
      val mappedOption = fmap(Some(4):Option[Int])(_ + 1) // Some(5)
      println(mappedList, mappedOption)
    }
  }

Recall the earlier Map example written in Golang, where the Map function can be seen as a unification of a family of similar functions for the array generic collection type (i.e. Map[A, B any] can be specialized into MapIntToInt, MapStringToBool etc..). The fmap function written in Scala above takes a step further: it unifies similar map methods for a family of generic collections (i.e. fmap[T[_], A, B](t: T[A]) can be specialized into fmapArrayIntToInt, fmapArrayStringToBool, fmapListIntToInt, fmapListStringToBool etc…). Higher kinded type gives us programmers a whole new level of separation of concerns to work with.

Higher ranked polymorphism

Another aspect where we can even be more polymorphic is the instantiation of the type parameters themselves. With vanilla generics, or even with higher kinded type, at the end of the day the use site of a generic value must be monomorphizable (even if you implement generics using type erasure), meaning you have to instantiate all type variables so that you always eventually end up with monomorphic type. Higher ranked polymorphism lifts this restriction for generic functions in particular.

The only language used in industry with support for higher ranked polymorphism is Haskell, so let’s take a look at a simple example where we want a function that takes a list transformation, then applies it to a list of b and a list of c. A naive implementation would look like this:

 transform2Lists :: ([a] -> [a]) -> [b] -> [c] -> ([b],[c])
 transform2Lists f bList cList = (f bList, f cList) -- compilation error

The reason this fails to compile is because the compiler is unable to unify a with b (and c too, but b is where the type error occurs first). That is because at call site, the caller would have to instantiate a, b, c with concrete types, and each of them could be a different type. The compiler can’t assume anything about all three, much less unifying them. The f function could be a generic function, but when passed to transform2Lists, its type variable a would still have to be instantiated with a concrete type, just like the type variable b and c of the two lists also being passed to transform2Lists. What we really want here is to be able to pass f as a polymorphic function at call site:

  transform2Lists :: (forall a. [a] -> [a]) -> [b] -> [c] -> ([b],[c])
  transform2Lists f bList cList = (f bList, f cList) 
  -- transform2Lists reverse [1,2,3] ["a","b","c"] => ([3,2,1],["c","b","a"])

The type of the function f that transform2Lists expects is now forall a. a -> a, meaning f is polymorphic at the call site of transform2Lists and will only be instantiated into monomorphic function at call sites (plural!) in the body of transform2Lists (i.e. f bList, f cList). Normal generic is called rank 1 polymorphism, and the type of transform2Lists is what we call a rank 2 polymorphic type, since you can pass a rank 1 polymorphic type as argument to transform2Lists.

Notice the forall a. in the type signature, and recall the connection we made between generics and logic. There is a correspondence between type systems and logic systems called the “Curry-Howard correspondence”, and a type system with higher ranked polymorphism corresponds to higher order predicate logic. Normal type system with vanilla generics corresponds to the familiar first order predicate logic we learned and used in high school’s math classes.

Conclusion

We are finally at the end of our rather lengthy tour (is it actually almost a journey at this point?) across the land of generics. We brushed up the foundation of polymorphism and dive deeper into parametric polymorphism – generics – in particular, and how it interplays and coexists with other kinds of polymorphism via type bounds and variances. We then investigated how generics are typically implemented, and what implications the implementation approaches have over the performance of our generic code. Then we went a bit beyond the realm of everyday programming and ventured into the land of higher kinded type and higher ranked polymorphism, both advanced and very powerful type system features rarely encountered in mainstream programming languages. As engineers at zen8labs, we celebrate the use of programming language’s type system to ensure code safety, correctness and clarity, and furthermore to leverage type system as a design tool whenever the language of choice allows us to. At the end of the day, our goal is to consistently deliver reliable, maintainable and valuable software for our customers, and with generics in our toolset, we can confidently look forward to consistently meet that goal.

For more insight, have a look at what zen8labs has to offer!

Anh Ngo, Software Engineer